Coding Tree

外观

爬楼梯 ​

问题 ​

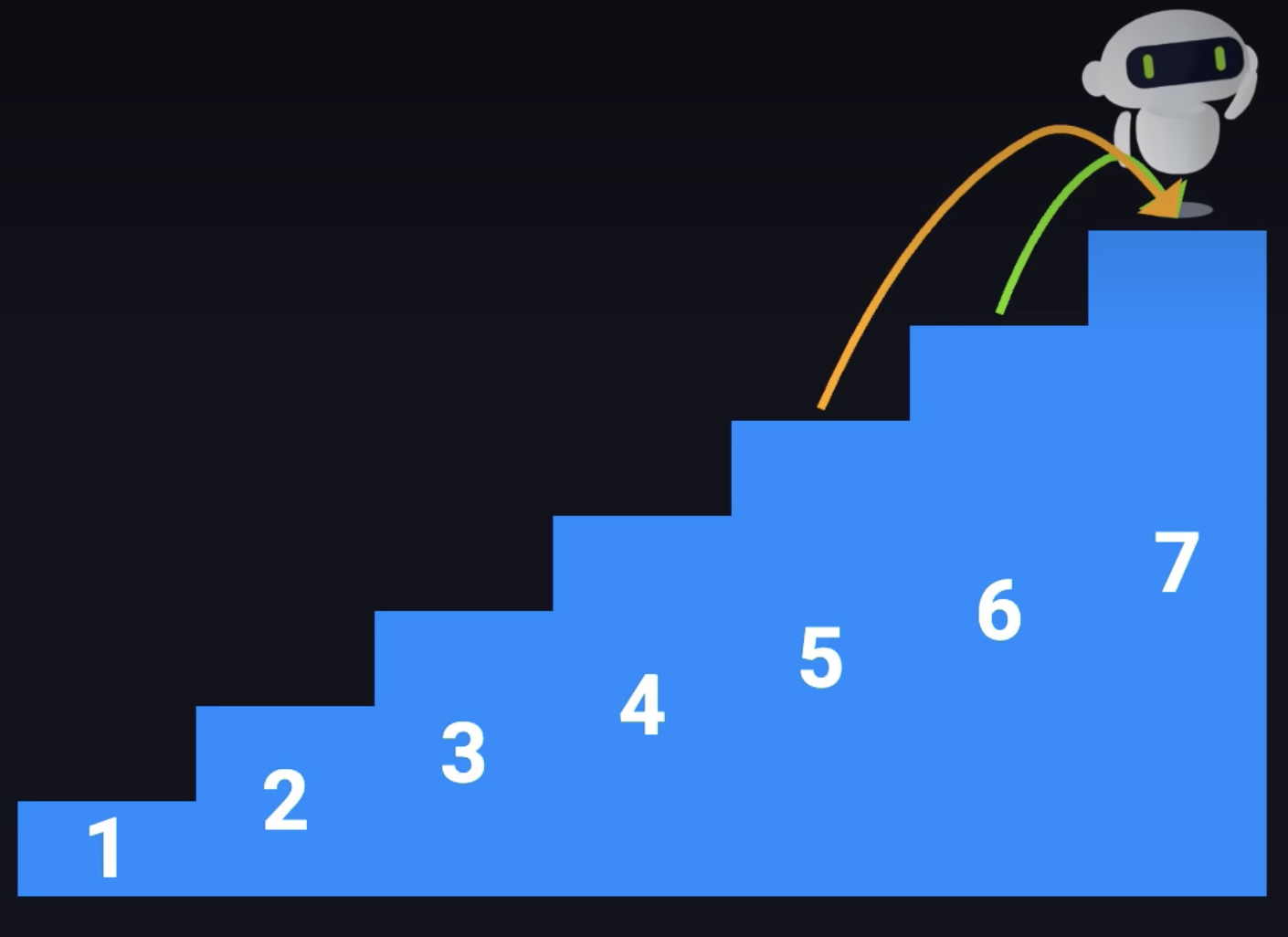
你在一个有n级台阶的楼梯底部，每次你可以选择爬1级或2级台阶，你有多少种不同的方法可以爬到楼梯顶部

分析 ​

shell
如果有1个台阶，有1种走法：
一次走1级

如果有2个台阶，有2种走法：
一次走1级
一次走2级

如果有3个台阶，有3种走法：
走3次1级
先走1级，再走2级
先走2级，再走1级

如果有4个台阶，有2种走法能够到达第4级台阶：
可以从第3级台阶走1级到达第4级
可以从第2级台阶走2级到达第4级

走到第3级台阶的走法有3
走到第2级台阶的走法有2

所以，走到第4级台阶的走法有 2 + 3 = 5 种

数据汇总如下

台阶数走法
11
22
33
45

这是一个菲波那切数列，可以得到递推公式

shell
f(n) = f(n-1) + f(n-2)

解法 ​

解法1：自底向上的动态规划（表格法） ​

该方法是最优解，空间复杂度O(1)，时间复杂度O(n)

python
def climbStairs(n):
    if n <= 2:
        return n

    a, b = 1, 2
    for _ in range(3, n + 1):
        a, b = b, a + b

    return b

解法2：递归 ​

满足动态规划特点：

  • 重复子问题
  • 最优子结构
python
def climbStairs(n):
    if n <= 2:
        return n
    return climbStairs(n - 1) + climbStairs(n - 2)

效率比较低

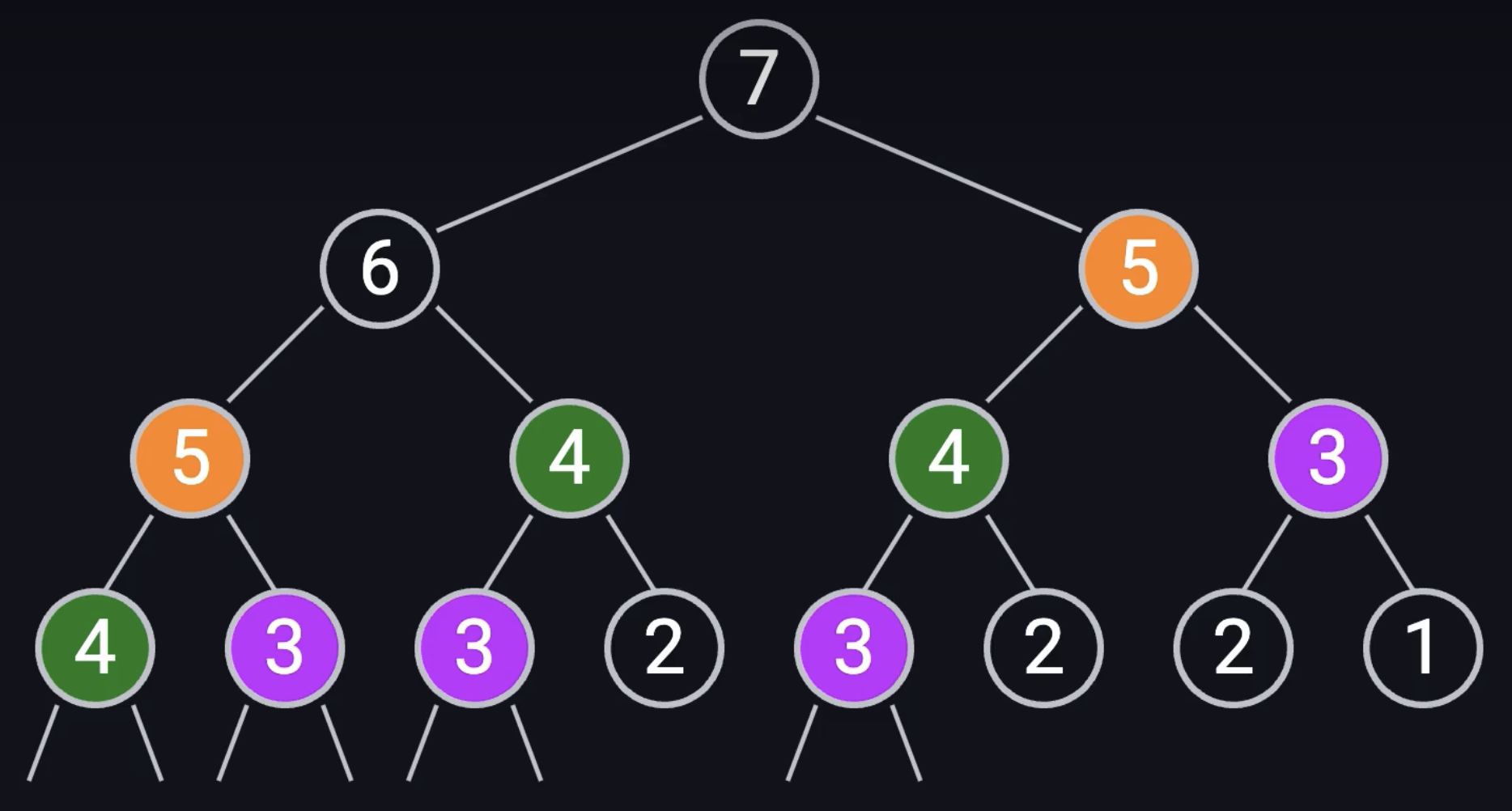
解法3：自顶向下的动态规划（记忆化） ​

python
def climbStairs(n, memo={}):
    if n in memo:
        return memo[n]

    if n <= 2:
        return n

    memo[n] = climbStairs(n - 1, memo) + climbStairs(n - 2, memo)
    return memo[n]