打家劫舍
问题
一排房子,每间都有钱,但不能偷相邻的。怎么才能偷得最多?
分析
场景1:
cpp
房间金额:2 7 9 3
第1种:2 + 9 = 11
第2种:7 + 3 = 10
11 > 10,取第1种场景2:
cpp
房间金额:10 1 1 5
最优选择:10 + 5 = 15解法
方法1:自底向上的分析(表格法)
cpp
2 7 9 3 1 5 8
如果只有1间房子: f(1) = 2
如果只有2间房子: f(2) = 7
如果只有3间房子: f(3) = 9 + 2 = 11
如果只有4间房子: f(4) = max(f(2) + 3, f(3)) = 11
可选方案1 偷:f(2) + 3
可选方案2 不偷:f(3)
...
f(i) = max(f(i-1), f(i-2) + nums[i])汇总如下
| f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) |
|---|---|---|---|---|---|---|
| 2 | 7 | 9 | 3 | 1 | 5 | 8 |
| 2 | 7 | 11 | 11 | 12 | 16 | 20 |
每次都选择收益最大的值
代码实现
- 时间复杂度
O(n) - 空间复杂度
O(1)
python
def rob(nums):
"""
f(i) = max(f(i-1), f(i-2) + nums[i])
"""
# 如果房子数为空
if not nums:
return 0
# 如果房子数为1,直接返回
if len(nums) == 1:
return nums[0]
# 处理普通情况
prev2 = nums[0]
prev1 = max(nums[0], nums[1])
for i in range(2, len(nums)):
current = max(prev1, prev2 + nums[i])
prev2 = prev1
prev1 = current
return prev1
def main():
nums = [2, 7, 9, 3, 1, 5, 8]
ret = rob(nums)
print("max ret: {}".format(ret))
if __name__ == "__main__":
main()运行结果
shell
$ python3 demo.py
max ret: 20方法2:自顶向下的动态规划(递归)
效率较低,时间复杂度:O(2^n)
python
def rob_recursive(nums, i):
"""
f(i) = max(f(i-1), f(i-2) + nums[i])
"""
if i < 0:
return 0
return max(rob_recursive(nums, i - 1), rob_recursive(nums, i - 2) + nums[i])
def main():
nums = [2, 7, 9, 3, 1, 5, 8]
ret = rob_recursive(nums, len(nums) - 1)
print("max ret: {}".format(ret))
if __name__ == "__main__":
main()shell
$ python3 demo.py
max ret: 20存在大量的重复计算
cpp
rob_recursive(6)
rob_recursive(5)
rob_recursive(4)
rob_recursive(3)
rob_recursive(2)
rob_recursive(1) + nums[2]
rob_recursive(1) + nums[3]
rob_recursive(2) + nums[4]
rob_recursive(1) + nums[2]
rob_recursive(3) + nums[5]
rob_recursive(2)
rob_recursive(1) + nums[2]
rob_recursive(1) + nums[3]
rob_recursive(4) + nums[6]
rob_recursive(3)
rob_recursive(2)
rob_recursive(1) + nums[2]
rob_recursive(1) + nums[3]
rob_recursive(2) + nums[4]
rob_recursive(1) + nums[2]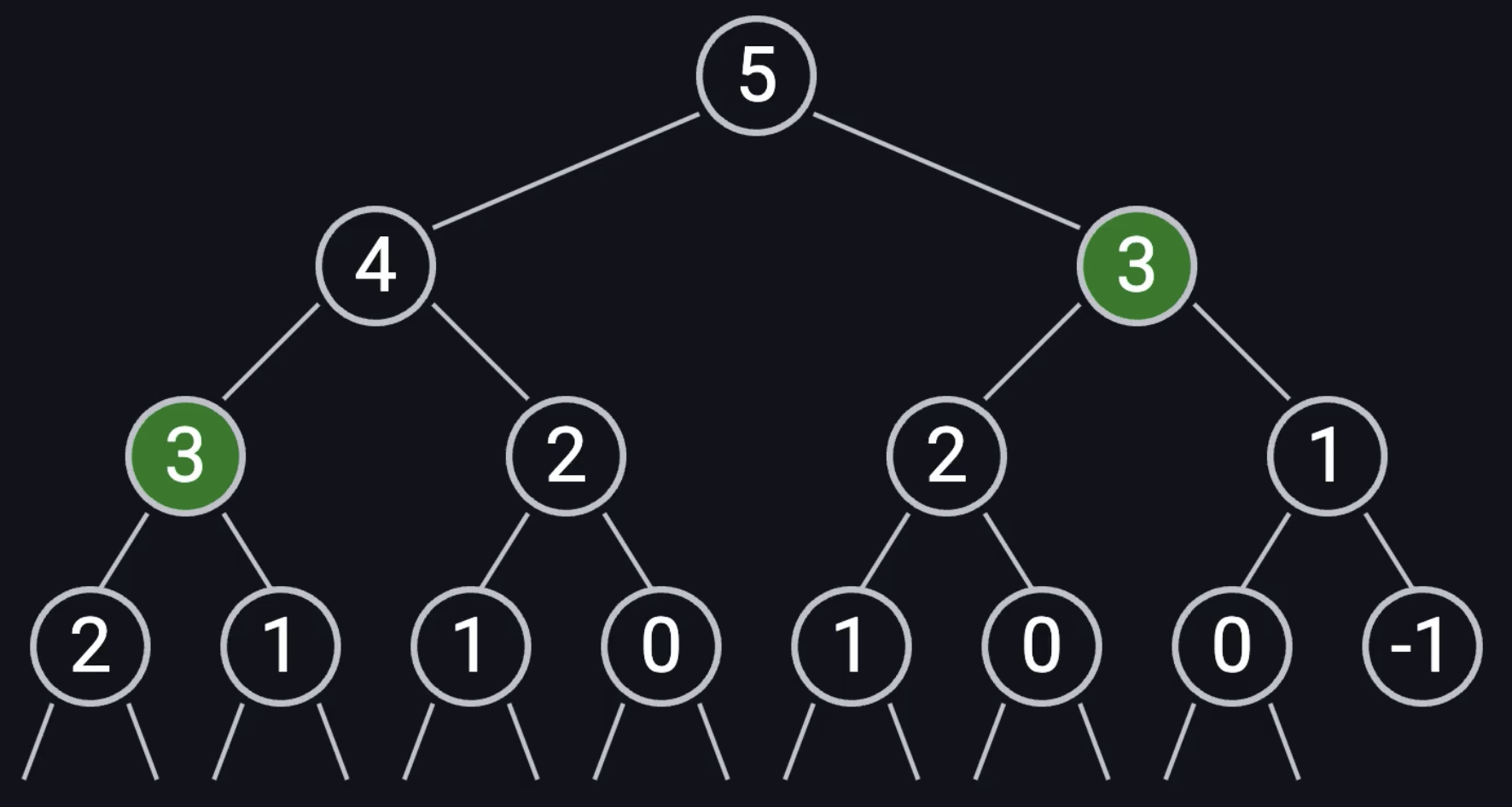
方法3:自顶向下的动态规划(递归+记忆化)
- 时间复杂度
O(n) - 空间复杂度
O(n)
python
def rob(nums):
"""
f(i) = max(f(i-1), f(i-2) + nums[i])
"""
memo={} # 保存计算过的问题
def dp(i):
if i < 0:
return 0
if i in memo:
return memo[i]
memo[i] = max(dp(i - 1), dp(i - 2) + nums[i])
return memo[i]
return dp(len(nums) - 1)
def main():
nums = [2, 7, 9, 3, 1, 5, 8]
ret = rob(nums)
print("max ret: {}".format(ret))
if __name__ == "__main__":
main()运行结果
shell
$ python3 demo.py
max ret: 20总结
动态规划两个特征
- 重叠子问题
- 最优子结构