动态规划入门
动态规划 Dynamic Programming (简称DP)
兔子树问题
题目:有一对兔子,从第一个月开始繁殖,每对兔子从出生后第二个月起,每个月都会生一对新兔子,假设,兔子寿命无限长
问题:一年后会有多少对兔子?
shell
第-2月 0
第-1月 1
第0月 1
第1月 2
第2月 3
第3月 5
第4月 8
第5月 13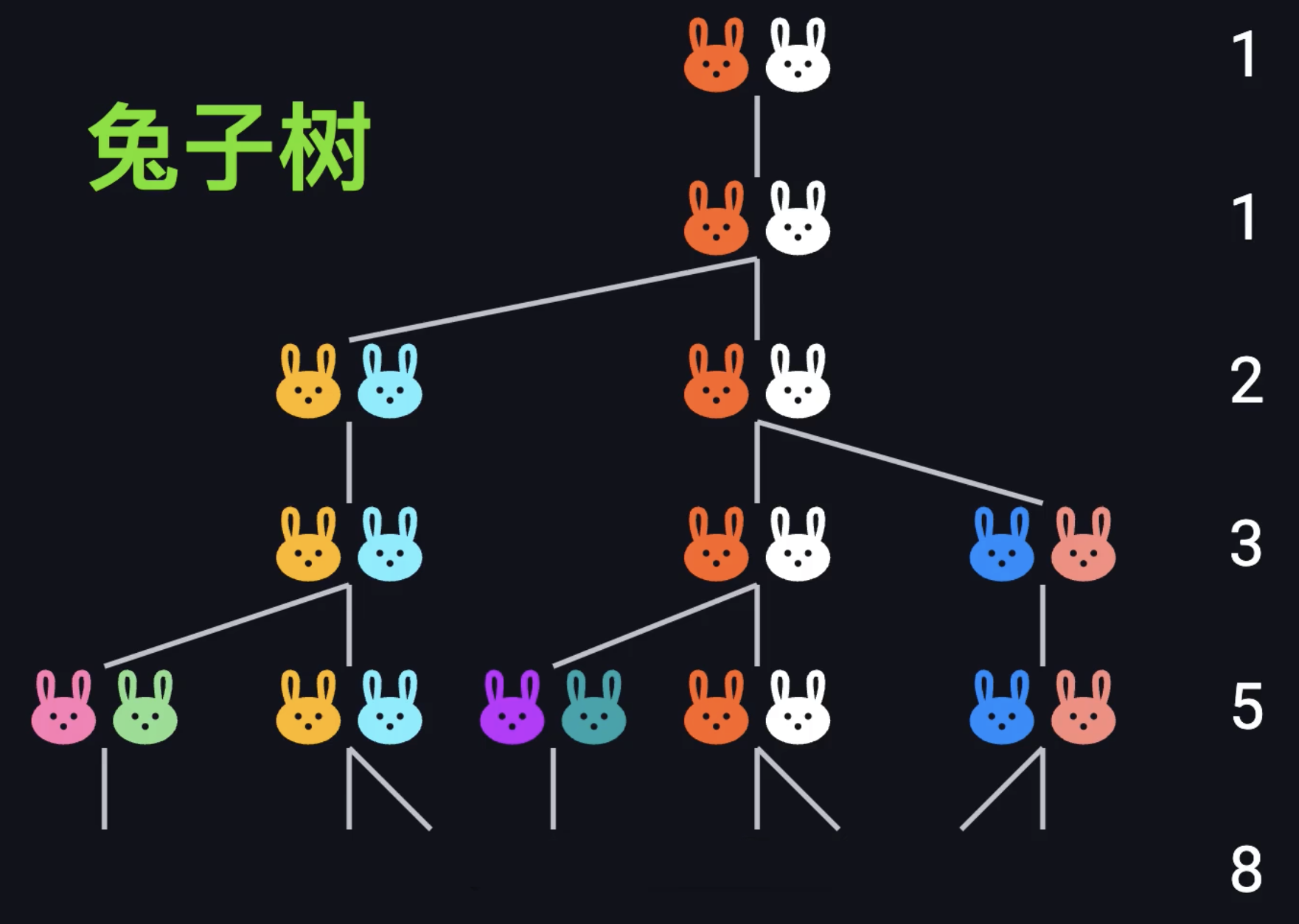
菲波那切数列
第1项是0,第2项是1,从第3项开始,每一项是前两项之和
shell
f(0) = 0
f(1) = 1
f(2) = f(1) + f(0) = 2
f(3) = f(2) + f(1) = 3
f(4) = f(3) + f(2) = 5
f(5) = f(4) + f(3) = 8
f(6) = f(5) + f(4) = 13
...
f(n) = f(n-1) + f(n-2)面试题:求菲波那切数列第n项
版本1:递归
实现代码
python
def fib(n):
if n <= 1:
return n
return fib(n - 1) + fib(n - 2)完整代码
python
# demo.py
def fib(n):
if n <= 1:
return n
return fib(n - 1) + fib(n - 2)
def main():
n = 40
ret = fib(n)
print(n, ret)
if __name__ == "__main__":
main()运行结果
shell
$ time python3 demo.py
40 102334155
python3 demo.py 14.26s user 0.08s system 97% cpu 14.651 total存在问题:会重复计算,即:重叠子问题
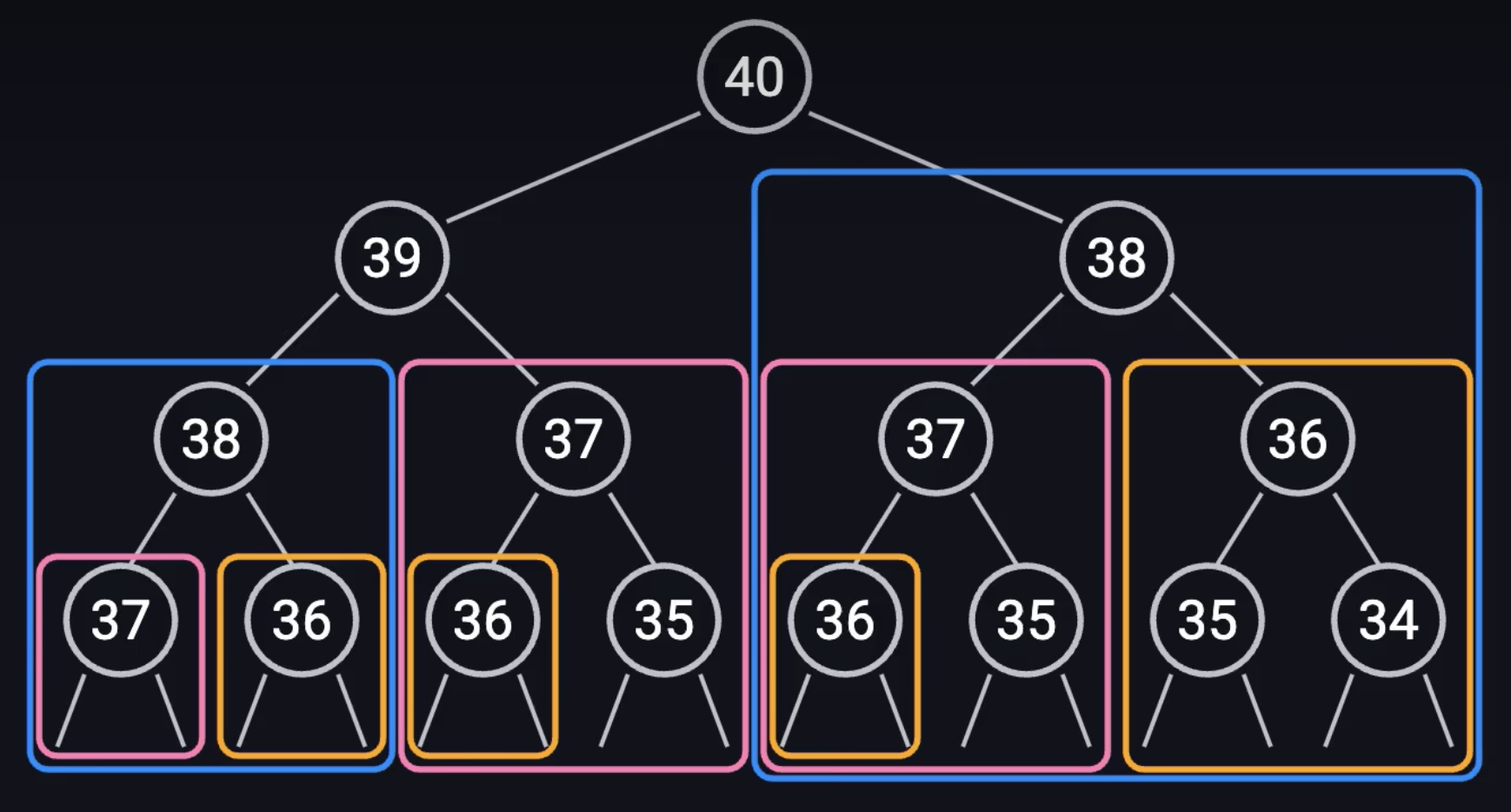
当n越大,重复的子问题越多,浪费的时间也就越多
重叠子问题:递归过程中,同一个子问题被重复求解了多次
版本2:自顶向下的动态规划(记忆化)
动态规划方式一:递归 + 记忆化
记忆化搜索:缓存已经计算过的子问题的值,后续遇到相同的子问题时,直接查缓存
优化代码
python
def fib(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fib(n - 1, memo) + fib(n - 2, memo)
return memo[n]完整代码
python
# demo.py
def fib(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = fib(n - 1, memo) + fib(n - 2, memo)
return memo[n]
def main():
n = 40
ret = fib(n)
print(n, ret)
if __name__ == "__main__":
main()运行结果
shell
$ time python3 demo.py
40 102334155
python3 demo.py 0.03s user 0.01s system 89% cpu 0.043 total可以看到,时间从14.651s 优化到了0.043s
版本3:自底向上的动态规划(表格法)
动态规划方式二:不使用递归
表格法(Tabulation):从最小的子问题出发,逐步计算
优化代码
python
def fib(n):
if n <= 1:
return n
dp = [0, 1]
for i in range(2, n + 1):
dp.append(dp[i - 1] + dp[i - 2])
return dp[n]完整代码
python
def fib(n):
if n <= 1:
return n
dp = [0, 1]
for i in range(2, n + 1):
dp.append(dp[i - 1] + dp[i - 2])
return dp[n]
def main():
n = 40
ret = fib(n)
print(n, ret)
if __name__ == "__main__":
main()运行结果
shell
$ time python3 demo.py
40 102334155
python3 demo.py 0.03s user 0.02s system 89% cpu 0.050 total版本4: 自底向上的动态规划(空间优化)
空间优化:不保存整个数组,空间复杂度,从O(n)降低到了O(1)
优化代码
python
def fib(n):
if n <= 1:
return n
a, b = 0, 1
for _ in range(2, n + 1):
a, b = b, a + b
return b完整代码
python
def fib(n):
if n <= 1:
return n
a, b = 0, 1
for _ in range(2, n + 1):
a, b = b, a + b
return b
def main():
n = 40
ret = fib(n)
print(n, ret)
if __name__ == "__main__":
main()运行结果
shell
$ time python3 demo.py
40 102334155
python3 demo.py 0.03s user 0.01s system 87% cpu 0.049 total总结

1、动态规划核心判断标准:
- 重复子问题
- 最优子结构:一个问题的最优解,可有由其子问题的最优解组合而成
2、适用题型:
- 爬楼梯
- 打家劫舍
- 最长公共子序列
- 零钱兑换
- 字符串拆分
- 0-1背包问题
3、不适用题型:
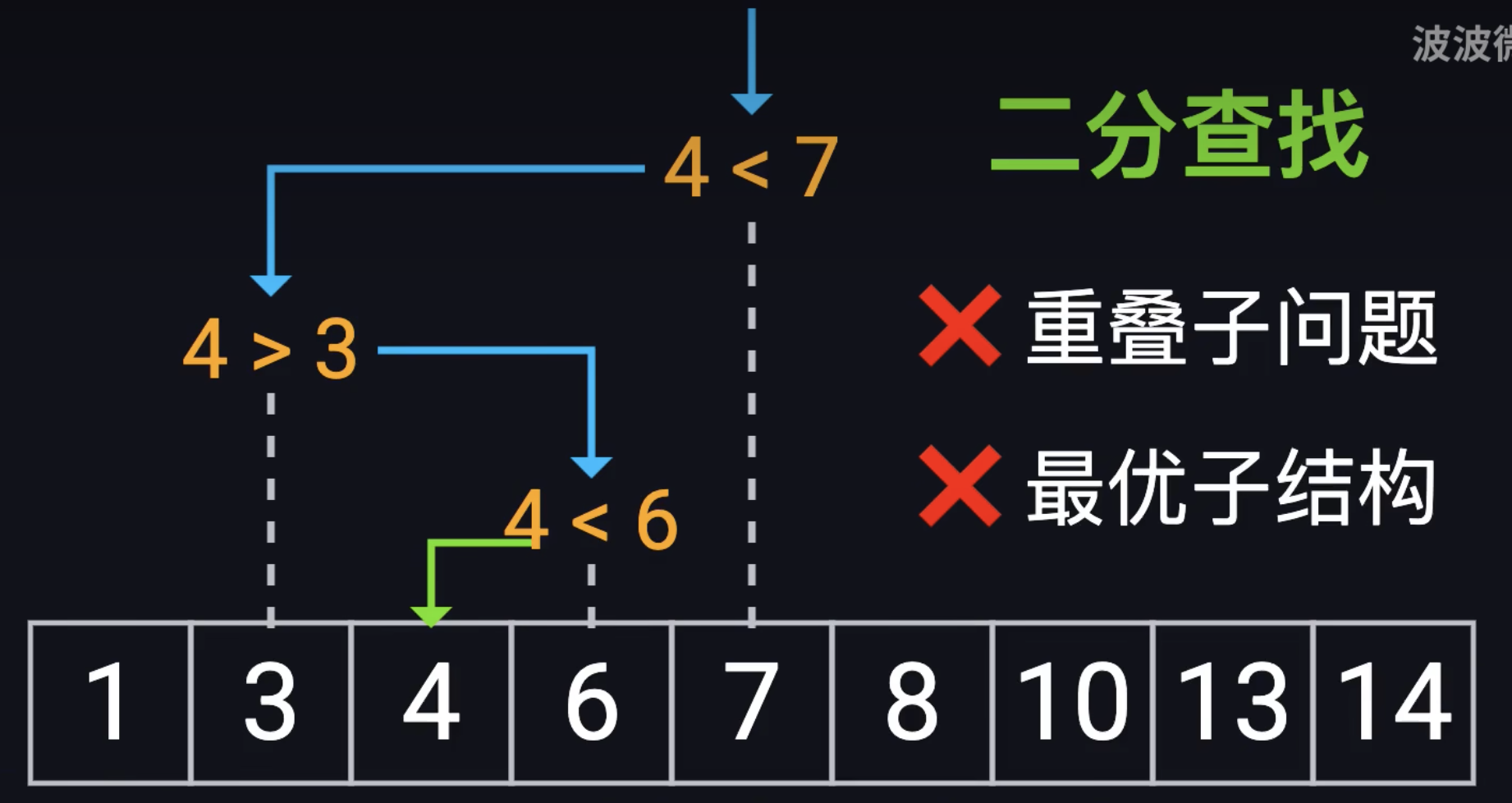
二分查找