Java面试题-查找排序
二分查找法
编写二分查找代码
前提: 有已排序数组
A(假设已经做好)定义左边界
L、右边界R,确定搜索范围,循环执行二分查找(3、4两步)获取中间索引
M=Floor((L+R) /2)中间索引的值
A[M]与待搜索的值T进行比较- ①
A[M]==T表示找到,返回中间索引 - ②
A[M]>T,中间值右侧的其它元素都大于T,无需比较,中间索引左边去找,M-1设置为右边界,重新查找 - ③
A[M]<T,中间值左侧的其它元素都小于T,无需比较,中间索引右边去找,M+1设置为左边界,重新查找
- ①
当
L>R时,表示没有找到,应结束循环
代码实现
public class BinarySearch {
public static void main(String[] args) {
int[] array = {1, 5, 6, 8, 10, 20, 30};
int target = 10;
System.out.println(binarySearch(array, target));
}
/**
* 二分查找,找到元素返回索引,找不到返回-1
* @param array
* @param target
* @return
*/
public static int binarySearch(int[] array, int target) {
// 左边指针
int left = 0;
// 右边指针
int right = array.length - 1;
// 中间指针
int middle;
while (left <= right) {
// 需要注意:此处可能会发生整数溢出
middle = (left + right) / 2;
if (array[middle] == target) {
return middle;
} else if (array[middle] > target) {
right = middle - 1;
}else {
left = middle + 1;
}
}
return -1;
}
}整数溢出问题
package com.demo;
public class IntegerOverflow {
public static void main(String[] args) {
int left = 0;
int right = Integer.MAX_VALUE;
int middle = (left + right) / 2;
System.out.println(middle);
// 1073741823
// 移动左指针
left = middle + 1;
middle = (left + right) / 2;
System.out.println(middle);
// -536870912
}
}整数溢出解决
1、方式一:
推导过程
(left + right) / 2
= left / 2 + right / 2
= left - left/2 + right / 2
= left + (-left/2 + right / 2)
= left + (right - left)/ 2
即:
(left + right) / 2 == left + (right - left)/ 2改进后的方法
package com.demo;
public class IntegerOverflow {
public static void main(String[] args) {
int left = 0;
int right = Integer.MAX_VALUE;
//int middle = (left + right) / 2;
int middle = left + (right - left)/ 2;
System.out.println(middle);
// 1073741823
left = middle + 1;
//middle = (left + right) / 2;
middle = left + (right - left)/ 2;
System.out.println(middle);
// 1610612735
}
}2、方式二:
使用无符号右移运算
package com.demo;
public class IntegerOverflow {
public static void main(String[] args) {
int left = 0;
int right = Integer.MAX_VALUE;
//int middle = (left + right) / 2;
//int middle = left + (right - left)/ 2;
int middle = (left + right) >>> 1;
System.out.println(middle);
// 1073741823
left = middle + 1;
//middle = (left + right) / 2;
//middle = left + (right - left) / 2;
middle = (left + right) >>> 1;
System.out.println(middle);
// 1610612735
}
}相关面试题
解题规则
- 奇数二分取中间
- 偶数二分取中间靠左
1、(京东实习生招聘)有一个有序表为 1,5,8,11,19,22,31,35,40,45,48,49,50 当二分査找值为 48 的结点时,查找成功需要比较的次数
答案:4次
解题:
第1次查找13/2= 6+1 = 7
1,5,8,11,19,22,[31],35,40,45,48,49,50
第2次查找6/2= 3
35,40,[45],48,49,50
第3次查找3/2= 1 + 1 = 2
48,[49],50
第4次查找
482、(美团点评校招)使用二分法在序列 1,4,6,7,15,33,39,50,64,78,75,81,89,96 中查找元素 81 时,需要经过( )次比较
答案:4次
解题:
第1次查找14/2=7
1,4,6,7,15,33,[39],50,64,78,75,81,89,96
第2次查找7/2= 3 + 1 =4
50,64,78,[75],81,89,96
第3次查找3/2= 1 + 1 =2
81,[89],96
第4次查找
813、(北京易道博识社招)在拥有128个元素的数组中二分查找一个数,需要比较的次数最多不超过多少次
答案:7次
常规解题,适用于数据较小的情况
128 / 2 = 64
64 / 2 = 32
32 / 2 = 16
16 / 2 = 8
8 / 2 = 4
4 / 2 = 2
2 / 2 = 1对数求解
2^n = 128
转换为:
log2(128) = log10(128) / log10(2)
向上取整得到最终结果
$ echo 'l(128)/l(2)' | bc -l
7.00000000000000000007注意事项
- 目前介绍的二分查找是以jdk 中
Arrays.binarySearch的实现作为讲解示范,后续选择题的解答思路也是以此为准 - 但实际上,二分查找有诸多变体,一旦使用变体的实现代码,则左右边界的选取会有变化,进而会影响之前选择题的答案选择
package java.util;
public class Arrays {
/**
* Searches a range of
* the specified array of ints for the specified value using the
* binary search algorithm.
* The range must be sorted (as
* by the {@link #sort(int[], int, int)} method)
* prior to making this call. If it
* is not sorted, the results are undefined. If the range contains
* multiple elements with the specified value, there is no guarantee which
* one will be found.
*
* @param a the array to be searched
* @param fromIndex the index of the first element (inclusive) to be
* searched
* @param toIndex the index of the last element (exclusive) to be searched
* @param key the value to be searched for
* @return index of the search key, if it is contained in the array
* within the specified range;
* otherwise, <tt>(-(<i>insertion point</i>) - 1)</tt>. The
* <i>insertion point</i> is defined as the point at which the
* key would be inserted into the array: the index of the first
* element in the range greater than the key,
* or <tt>toIndex</tt> if all
* elements in the range are less than the specified key. Note
* that this guarantees that the return value will be >= 0 if
* and only if the key is found.
* @throws IllegalArgumentException
* if {@code fromIndex > toIndex}
* @throws ArrayIndexOutOfBoundsException
* if {@code fromIndex < 0 or toIndex > a.length}
* @since 1.6
*/
public static int binarySearch(int[] a, int fromIndex, int toIndex,
int key) {
rangeCheck(a.length, fromIndex, toIndex);
return binarySearch0(a, fromIndex, toIndex, key);
}
/**
* Checks that {@code fromIndex} and {@code toIndex} are in
* the range and throws an exception if they aren't.
*/
private static void rangeCheck(int arrayLength, int fromIndex, int toIndex) {
if (fromIndex > toIndex) {
throw new IllegalArgumentException(
"fromIndex(" + fromIndex + ") > toIndex(" + toIndex + ")");
}
if (fromIndex < 0) {
throw new ArrayIndexOutOfBoundsException(fromIndex);
}
if (toIndex > arrayLength) {
throw new ArrayIndexOutOfBoundsException(toIndex);
}
}
// Like public version, but without range checks.
private static int binarySearch0(int[] a, int fromIndex, int toIndex,
int key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
int midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
}参数解释
a:要搜索的数组
fromIndex:指定范围的开始处索引(包含)
toIndex:指定范围的结束处索引(不包含)
key:要搜索的值
如果要搜索的元素key在指定的范围内,则返回搜索值的索引;否则返回-1或“-”(插入点)。
冒泡排序
一文详解十大经典排序算法 https://mp.weixin.qq.com/s/yNxBG9-Wa52VENggOt0zNw
面试题:排序
目标:
- 掌握常见排序算法(快排、冒泡、选择、插入等)的实现思路
- 手写冒泡、快排的代码
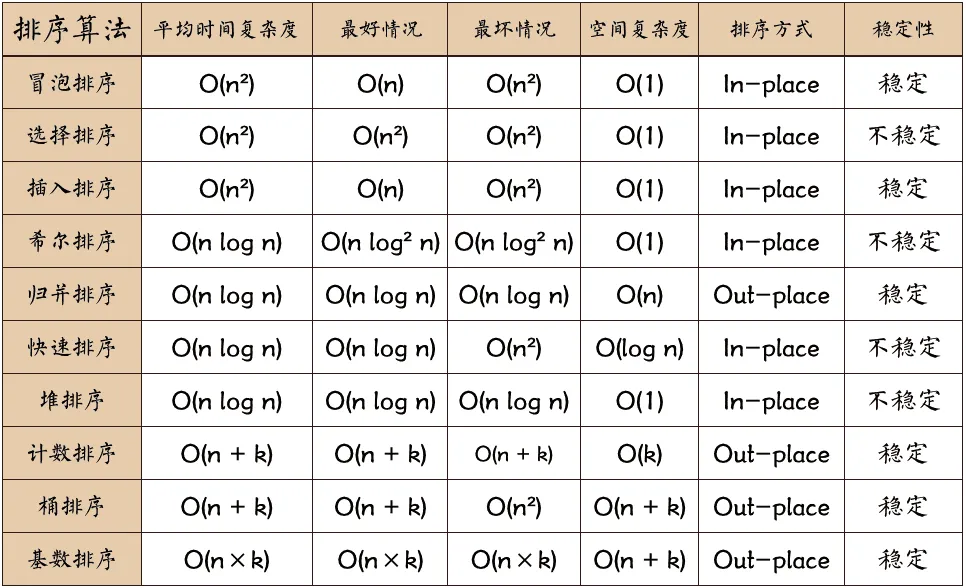
- 了解各个排序算法的特性,如时间复杂度、是否稳定
代码实现
package com.demo;
import java.util.Arrays;
public class BubbleSort {
public static void main(String[] args) {
int[] array = {5, 7, 4, 1, 3, 2, 8, 9};
bubbleSort(array);
System.out.println(Arrays.toString(array));
// [1, 2, 3, 4, 5, 7, 8, 9]
}
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
for (int j = 0; j < array.length - 1; j++) {
System.out.println("第" + (j + 1) + "次比较");
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
}
}
System.out.println("第" + (i + 1) + "轮排序:" + Arrays.toString(array));
}
}
public static void swap(int[] array, int i, int j) {
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}输出日志
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第1轮排序:[5, 4, 1, 3, 2, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第2轮排序:[4, 1, 3, 2, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第3轮排序:[1, 3, 2, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第4轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第5轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第6轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第7轮排序:[1, 2, 3, 4, 5, 7, 8, 9]第一次优化:减少比较次数
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
// 减少比较次数
for (int j = 0; j < array.length - 1 - i; j++) {
System.out.println("第" + (j + 1) + "次比较");
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
}
}
System.out.println("第" + (i + 1) + "轮排序:" + Arrays.toString(array));
}
}输出日志
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第1轮排序:[5, 4, 1, 3, 2, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第2轮排序:[4, 1, 3, 2, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第3轮排序:[1, 3, 2, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第4轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第5轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第6轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第7轮排序:[1, 2, 3, 4, 5, 7, 8, 9]第二次优化:减少冒泡次数
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
// 元素是否发生交换
boolean swapped = false;
for (int j = 0; j < array.length - 1 - i; j++) {
System.out.println("第" + (j + 1) + "次比较");
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
swapped = true; // 如果发生交换,认为排序没有完成
}
}
System.out.println("第" + (i + 1) + "轮排序:" + Arrays.toString(array));
if(!swapped){
break;
}
}
}输出日志
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第1轮排序:[5, 4, 1, 3, 2, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第2轮排序:[4, 1, 3, 2, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第3轮排序:[1, 3, 2, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第4轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第5轮排序:[1, 2, 3, 4, 5, 7, 8, 9]如果使用已经有序的数组排序,则只需要一轮比较就可以输出结果
int[] array = {1, 2, 3, 4, 5, 7, 8, 9};输出日志
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第1轮排序:[1, 2, 3, 4, 5, 7, 8, 9]第三次优化:减少比较次数
最优解
public static void bubbleSort(int[] array) {
int n = array.length - 1;
// 此处可以换成 while(true)
for (int i = 0; i < array.length - 1; i++) {
int last = 0;// 表示最后一次交换索引的位置
for (int j = 0; j < n; j++) {
System.out.println("第" + (j + 1) + "次比较");
if (array[j] > array[j + 1]) {
swap(array, j, j + 1);
last = j;
}
}
n = last;
System.out.println("第" + (i + 1) + "轮排序:" + Arrays.toString(array));
// 没有无序元素,直接跳出循环
if (n == 0) {
break;
}
}
}输出日志
第1次比较
第2次比较
第3次比较
第4次比较
第5次比较
第6次比较
第7次比较
第1轮排序:[5, 4, 1, 3, 2, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第4次比较
第2轮排序:[4, 1, 3, 2, 5, 7, 8, 9]
第1次比较
第2次比较
第3次比较
第3轮排序:[1, 3, 2, 4, 5, 7, 8, 9]
第1次比较
第2次比较
第4轮排序:[1, 2, 3, 4, 5, 7, 8, 9]
第1次比较
第5轮排序:[1, 2, 3, 4, 5, 7, 8, 9]冒泡排序思路
文字描述(以升序为例)
依次比较数组中相邻两个元素大小,若
a[i]>a[j+1],则交换两个元素,两两都比较一遍称为一轮冒泡,结果是让最大的元素排至最后重复以上步骤,直到整个数组有序
优化方式: 每轮冒泡时,最后一次交换索引可以作为下一轮冒泡的比较次数,如果这个值为零,表示整个数组有序,直接退出外层循环即可
选择排序
代码实现
package com.demo;
import java.util.Arrays;
public class SelectionSort {
public static void main(String[] args) {
int[] array = {5, 7, 4, 1, 3, 2, 8, 9};
//int[] array = {1, 2, 3, 4, 5, 7, 8, 9};
selectionSort(array);
System.out.println(Arrays.toString(array));
// [1, 2, 3, 4, 5, 7, 8, 9]
}
public static void selectionSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
// i代表每一轮选择最小元素要交换到的目标索引
int min = i; // 代表最小元素的索引
for (int j = min + 1; j < array.length; j++) {
if(array[min] > array[j]){
min = j;
}
}
if(min != i){
swap(array, min, i);
}
System.out.println(Arrays.toString(array));
}
}
public static void swap(int[] array, int i, int j) {
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}输出日志
[1, 7, 4, 5, 3, 2, 8, 9]
[1, 2, 4, 5, 3, 7, 8, 9]
[1, 2, 3, 5, 4, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]
[1, 2, 3, 4, 5, 7, 8, 9]排序思路
文字描述(以升序为例)
将数组分为两个子集,排序的和未排序的,每一轮从未排序的子集中选出最小的元素,放入排序子集
重复以上步骤,直到整个数组有序
优化方式
- 为减少交换次数,每一轮可以先找最小的索引,在每轮最后再交换元素
与冒泡排序比较
- 二者平均时间复杂度都是
O(n²) - 选择排序一般要快于冒泡,因为其交换次数少
- 但如果集合有序度高,冒泡优于选择
- 冒泡属于稳定排序算法,而选择属于不稳定排序
- 稳定排序:如果a原本在b前面,而a=b,排序后a仍然在b的前面
- 不稳定排序:如果a原本在b的前面,而a=b,排序后a可能会出现在b的后面
插入排序
代码实现
package com.demo;
import java.util.Arrays;
public class InsertSort {
public static void main(String[] args) {
int[] array = {5, 7, 4, 1, 3, 2, 8, 9};
//int[] array = {1, 2, 3, 4, 5, 7, 8, 9};
insertSort(array);
System.out.println(Arrays.toString(array));
// [1, 2, 3, 4, 5, 7, 8, 9]
}
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
// i 代表待插入元素索引
int t = array[i];
// 已排序区的元素
int j = i - 1;
while (j >= 0) {
if (array[j] > t) {
array[j + 1] = array[j];
} else {
//退出循环,减少比较次数
break;
}
j--;
}
// 插入元素
array[j + 1] = t;
}
}
}排序思路
文字描述(以升序为例)
- 将数组分为两个区域,排序区域和未排序区域,每一轮从未排序区域中取出第一个元素,插入到排序区域(需保证顺序)
- 重复以上步骤,直到整个数组有序
优化方式
- 待插入元素进行比较时,遇到比自己小的元素,就代表找到了插入位置,无需进行后续比较
- 插入时可以直接移动元素,而不是交换元素
与选择排序比较
- 二者平均时间复杂度都是
0(n^2) - 大部分情况下,插入都略优于选择
- 有序集合插入的时间复杂度为
0(n) - 插入属于稳定排序算法,而选择属于不稳定排序
希尔排序
略
插入和选择面试题
1、使用直接插入排序算法对序列18,23,19,9,23,15进行排序,第三趟排序后的结果为:
推演:
插入排序分为有序区和无序区
有序区:18
无序区:23,19,9,23,15
第1趟:18 23 | 19 9 23 15
第2趟:18 19 23 | 9 23 15
第3趟:9 18 19 23 | 23 15答案:9 18 19 23 23 15
2、使用直接选择排序算法对序列18,23,19,9,23,15进行排序,第3趟排序后的结果为:
推演:
每次从待排序队列取最小值,放入有序队列
第1趟:9 | 23 19 18 23 15
第2趟:9 15 | 19 18 23 23
第3趟:9 15 18 | 19 23 23答案:9 15 18 19 23 23
快速排序
文字描述
1、每一轮排序选择一个基准点(pivot)进行分区
- 让小于基准点的元素的进入一个分区,大于基准点的元素的进入另一个分区
- 当分区完成时,基准点元素的位置就是其最终位置
2、在子分区内重复以上过程,直至子分区元素个数少于等于 1,这体现的是分而治之的思想(divide-and-conguer)
实现方式
1、单边循环快排(lomuto 洛穆托分区方案)
- 选择最右元素作为基准点元素
- j指针负责找到比基准点小的元素,一旦找到则与i进行交换
- i指针维护小于基准点元素的边界,也是每次交换的目标索引
- 最后基准点与i交换,i即为分区位置
2、双边循环快排(并不完全等价于 hoare 霍尔分区方案)
- 选择最左元素作为基准点元素
- j指针负责从右向左找比基准点小的元素,i指针负责从左向右找比基准点大的元素,一旦找到二者交换,直至i,j相交
- 最后基准点与i(此时i与j相等)交换,i即为分区位置
3、双边循环几个要点
- 基准点在左边,并且要先j后i
while(i < j && a[j] > pv ) j--while(i < j && a[i] <= pv ) i++
代码实现
1、单边循环快排(lomuto 洛穆托分区方案)
递归版本
package com.demo;
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] array = {5, 3, 7, 2, 9, 8, 1, 4};
quickSort(array);
System.out.println(Arrays.toString(array));
// [1, 2, 3, 4, 5, 7, 8, 9]
}
private static void quickSort(int[] array) {
sort(array, 0, array.length - 1);
}
private static void sort(int[] array, int low, int high) {
if (low >= high) {
return;
}
// 找到中间数的索引值
int p = partition(array, low, high);
// 左边分区排序
sort(array, low, p - 1);
// 右边分区排序
sort(array, p + 1, high);
}
private static int partition(int[] array, int low, int high) {
int pv = array[high]; // 基准点元素
int i = low;
for (int j = low; j < high; j++) {
if (array[j] < pv) {
// 优化:如果索引不一样才需要交换
if (i != j) {
swap(array, i, j);
}
i++;
}
}
if (i != high) {
swap(array, i, high);
}
// 返回值是基准点元素的索引值
return i;
}
public static void swap(int[] array, int i, int j) {
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}2、双边循环快排(并不完全等价于 hoare 霍尔分区方案)
package com.demo;
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] arr = new int[]{1, 5, 9, 8, 7, 6};
quickSort(arr);
System.out.println(Arrays.toString(arr));
// [1, 5, 6, 7, 8, 9]
}
private static void quickSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
sort(arr, 0, arr.length - 1);
}
private static void sort(int[] arr, int low, int high) {
if (low >= high) {
return;
}
int pos = partition(arr, low, high);
sort(arr, low, pos - 1);
sort(arr, pos + 1, high);
}
private static int partition(int[] arr, int low, int high) {
int pv = arr[low];
int left = low;
int right = high;
while (left < right) {
// 从右找小
while (left < right && arr[right] > pv) {
right--;
}
// 从左找大
while (left < right && arr[left] <= pv) {
left++;
}
swap(arr, left, right);
}
swap(arr, low, right);
return right;
}
private static void swap(int[] arr, int i, int pos) {
int temp = arr[i];
arr[i] = arr[pos];
arr[pos] = temp;
}
}