第21章项目管理科学基础

21.1 工程经济学

21.1.1 资金的时间价值与等值计算

资金的时间价值与等值计算的概念

资金的时间价值是指不同时间发生的等额资金在价值上的差别

例如，在年利率为 5.22% 的条件下，当年的 100元与下一年的 105.22元是等值的，即

100×(1+5.22%)元= 105.22元

而当年的 100元又与上一年的 95.04元等值，即

100 /(1+5.22%)元 = 95.04元

可以认为在年利率为 5.22% 的情况下，当前的 100 元与一年后的 105.22 元是等值的，与一年前的 95.04 元也是等值的

利息、利率及其计算

F为本利和: P 为本金; I 为利息; n 表示计息期数

Fn= P + In

i为利率

i = (I / P ) * 100%

单利法: 利息不生利息

Fn = P + P * n * i = P * (1 + i * n)

复利法: 利息也生利息

Fn= P * (1 + i) ^ n

净现金流量

净现金流量 = CI- CO

CI为现金流入量; CO为现金流出量

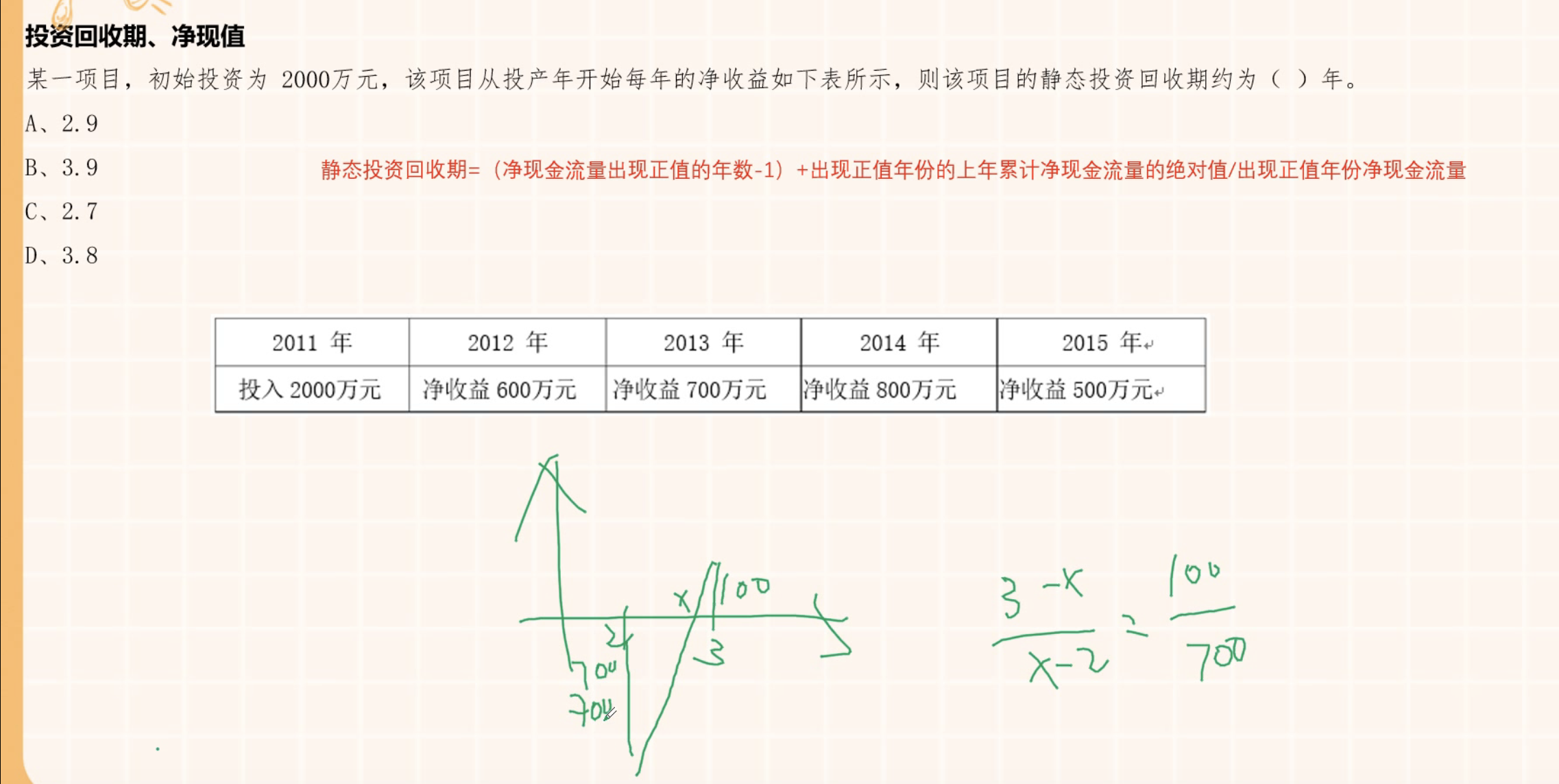
静态投资回收期

Pt = (累计净现金流量开始出现正值或零的年份数 - 1) + 上年累计净现金流量的绝对值 / 当年净现金流量

简化：
Pt = (正值年份 - 1) + 上年累计绝对值 / 当年值

计算思路：相似三角形

3. 资金的等值计算

21.1.2 项目经济评价

根据是否考虑资金的时间价值，投资项目经济评价方法可分为两类 :

静态评价
动态评价

1 静态评价方法

1 )静态投资回收期法

2 )投资收益率法

2 动态评价方法

1 )净现值法

2 )净现值率法

3 )费用现值法

动态投资回收期法 5 )内部收益率法

投资方案的选择

21.2 运筹学

21.2.1 线性规划

1 线性规划建模

21.2.2 运输问题

21.2.3 指派问题

21.2.4 动态规划

最短路径问题
资源分配问题

21.2.5 图与网络

最短路径问题
最小生成树

21.2.6 博弈论

21.2.7 决策分析

不确定型决策
风险型决策

考点

1、线性规划

画图取顶点值带入计算

1.1、例题：某工厂生产两种产品S和K，收到原材料供应和设备加工工时的限制。单个产品的利润、原材料消耗及加工工时如下表所示

为获得最大利润，S应生产（）件

产品	S	K	资源限制
原材料消耗（公斤/件）	10	20	120
设备工时（小时/件）	8	8	80
利润（元/件）	12	16

A. 7; B. 8; C. 9; D. 10;

解答：

条件：

10S + 20K <= 120
8S + 8K <= 80
S >= 0
K >= 0

求：max(12S + 16K)

化简

S + 2K <= 12
S + K <= 10
S >= 0
K >= 0

绘图

求出四条线的交点：

S + 2K = 12
S + K = 10

=> S = 10 - K
2K = 12 - (10 - K)
2K = 12 - 10 + K
K =2
=> (8, 2)

S + 2K == 12
S = 0
=>(0, 6)

S + 2K = 12
K = 0
=>(12, 0)

S + K = 10
S = 0
=> (0, 10)

S + K = 10
K = 0
=> (10, 0)

交点求值

求：max(12S + 16K)

(8, 2) => 12 * 8 + 16 * 2 = 96 + 32 = 128
(0, 6) => 16 * 6 = 96
(10, 0) => 12 * 10 = 120

排除不满足条件：
(12, 0) => 12 * 12 = 144
(0, 10) => 16 * 10 = 160

交点(8, 2)，max = 128，选B

2、动态规划

某公司现有400 万元用于投资甲、乙、丙三个项目，投资额以百万为单位，知甲、乙、丙三项投资的可能方案及相应获得的收益如下表所示:则该公司能够获得的最大收益值是 ( ) 百万元。

项目-收益-投资额	1	2	3	4
甲	4	6	9	10
乙	3	9	10	11
丙	5	8	11	15

A.17 B.18 C.20 D.21

解题思路：

（1）计算平均收益

项目-收益-投资额	1	2	3	4
甲	4	3	3	2.5
乙	3	4.5	3.3	2.7
丙	5	4	3.7	3.7

（2）选最大

丙 5 1 => 5
乙 4.5 2 => 9
甲 4 1=> 4

5 + 9 + 4 = 18

选B

3、最小生成树

断线法

3.1、煤气公司想要在某地区高层住宅楼之间铺设煤气管道并与主管道相连，位置如下图所示，节点代表各住宅的楼和主管道位置，线上数字代表两节点间距离(单位: 百米)，则煤气公司铺设的管道总长最短为()米。

A.1800 B.2200 C.2000 D.2100

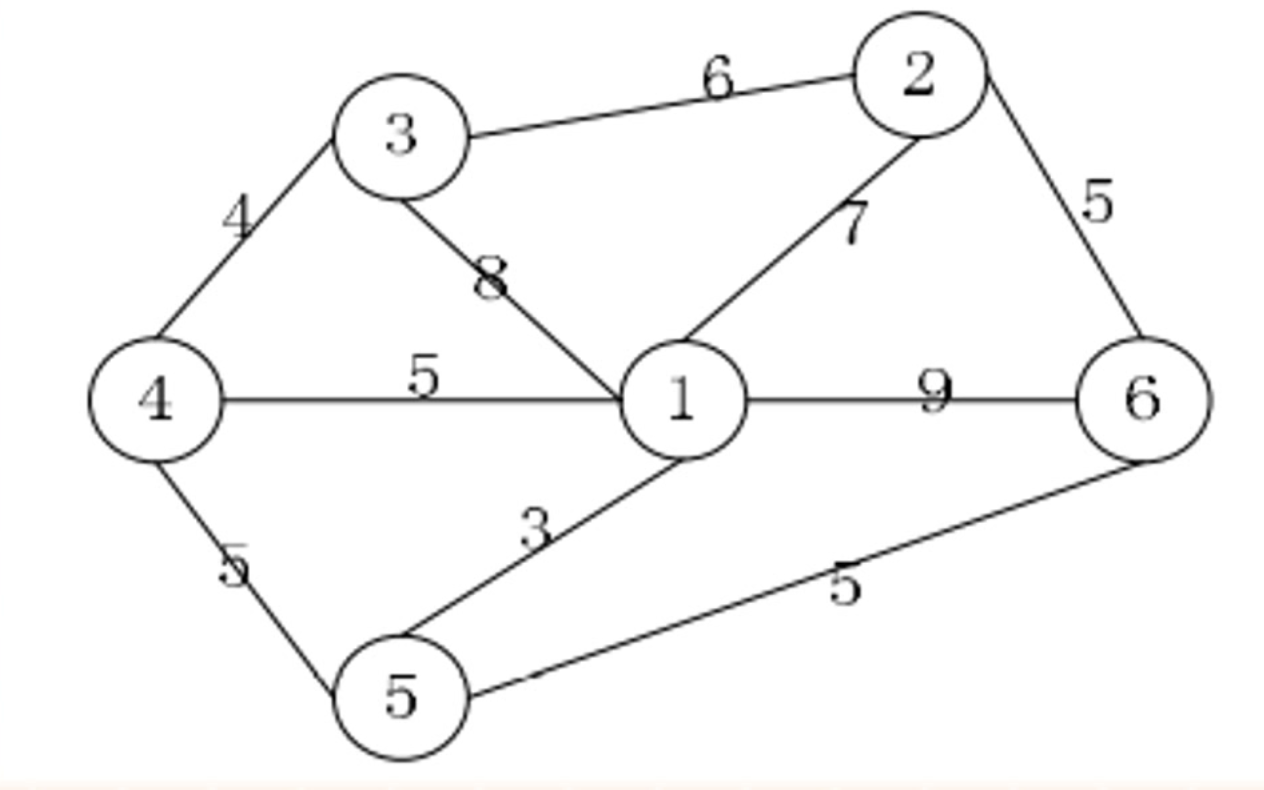
解题：

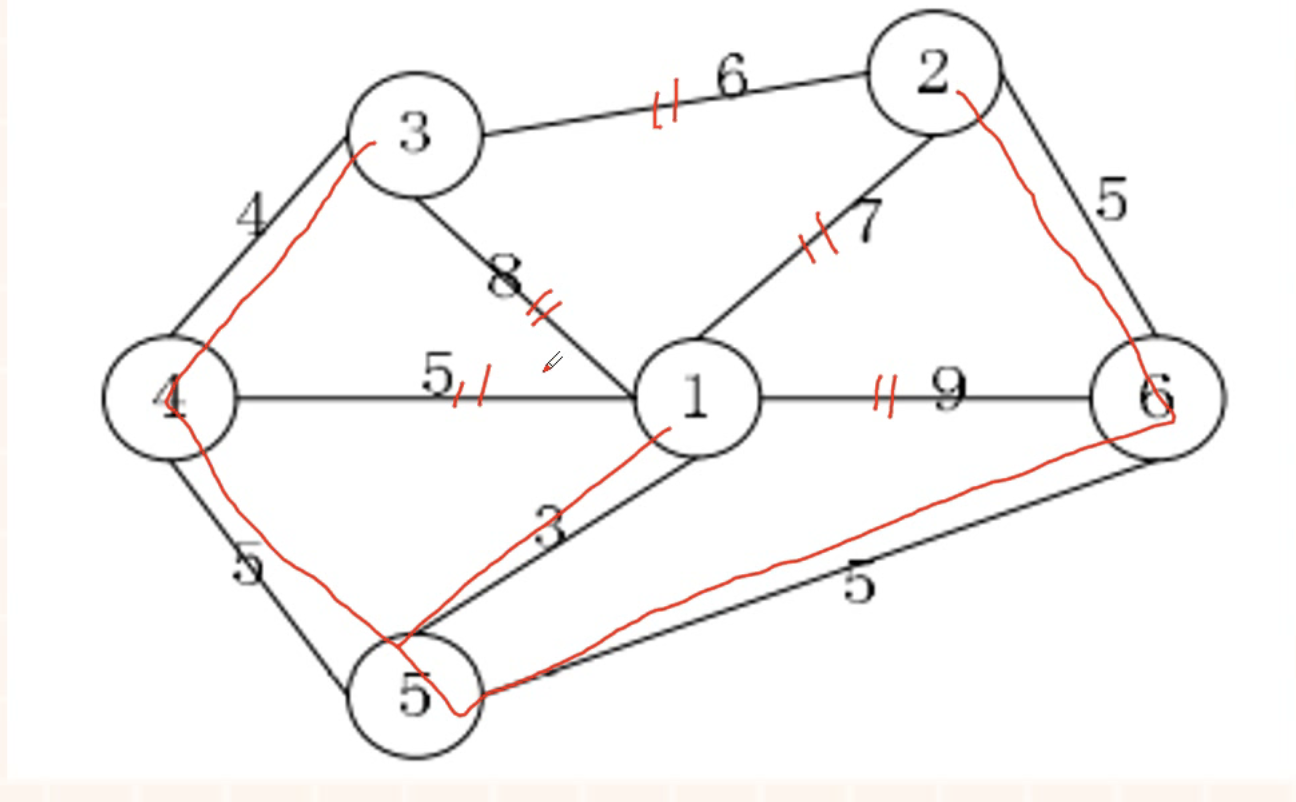
计算

4 + 5 + 3 + 5 + 5 = 22百米  = 2200 米

选择B

3.2、有8口海上油井，相互间距离如下表所示(单位:海里)。其中1号井离海岸最短长度，为5海里，先要从海岸经1号井铺设油管将各井连接起来，则铺设输油管道的最短长度()海里。

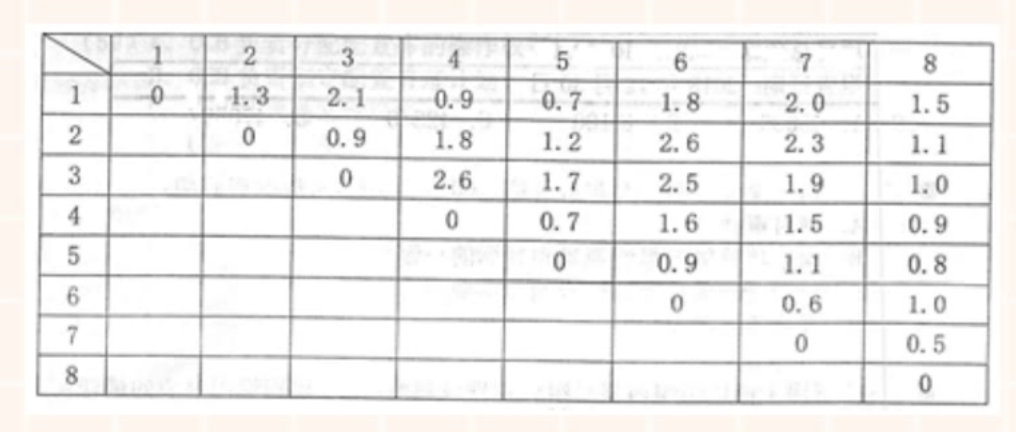
A.9.1 B.9.2 C.10.1 D.10.2

解题：

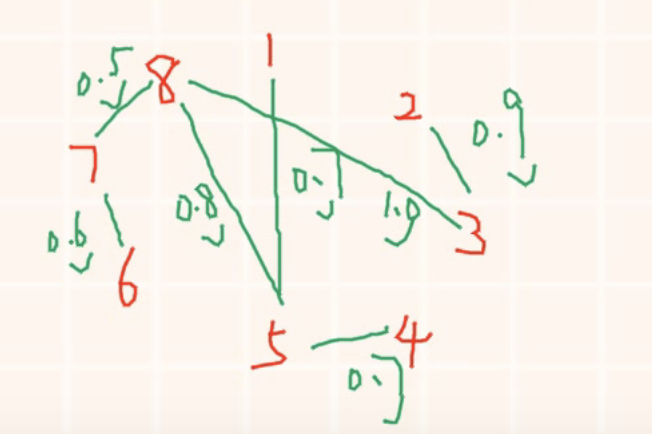
选D

3.3、下图为某地区的通信线路图，图中节点为8个城市，节点间标识的数字为城市间拟铺设通信线路的长度，为了保持8个城市通讯连接，则至少铺设 ()千米的线路。

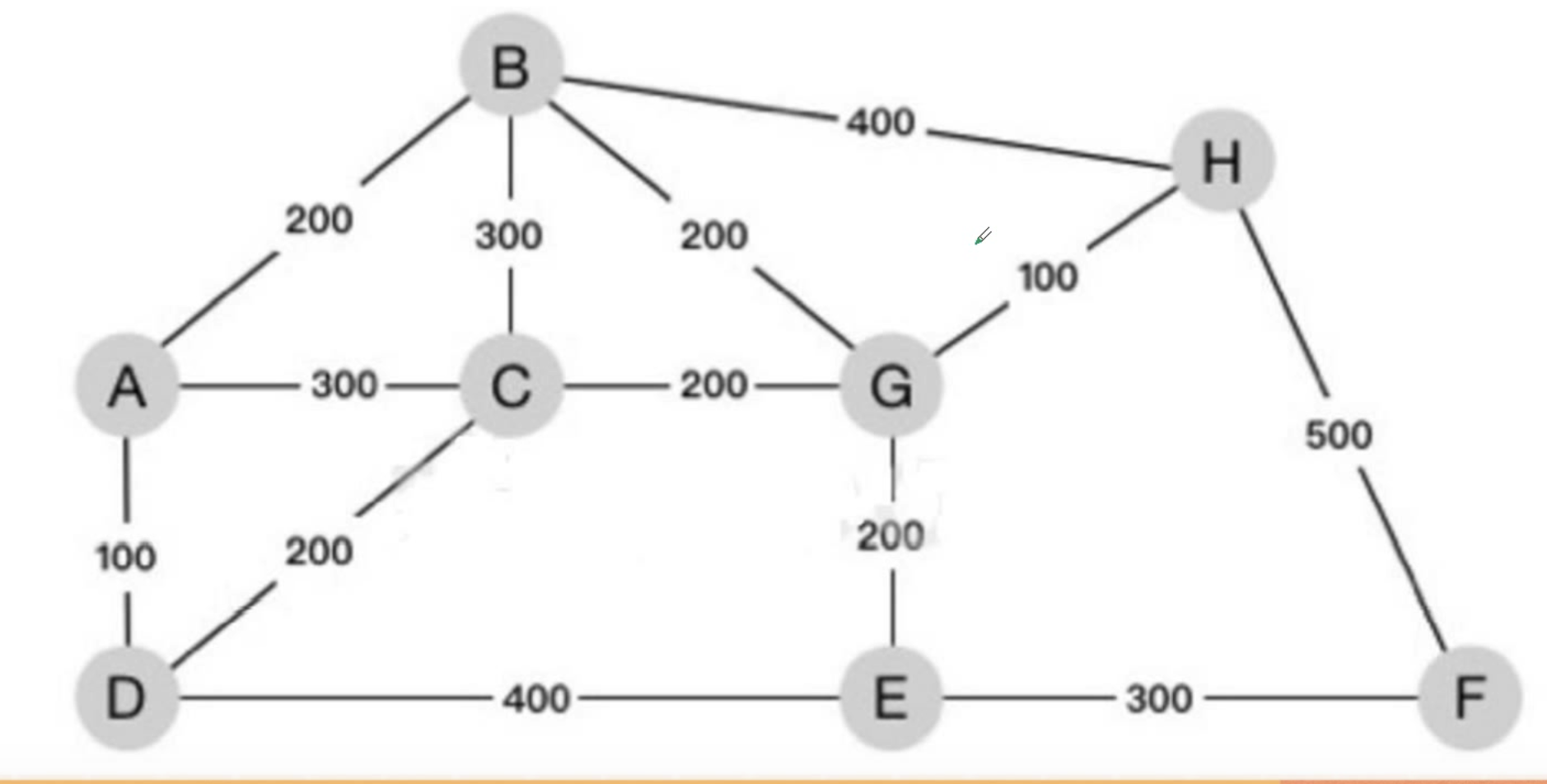
A.1000 B.1100 C.1200 D.1300

解题：

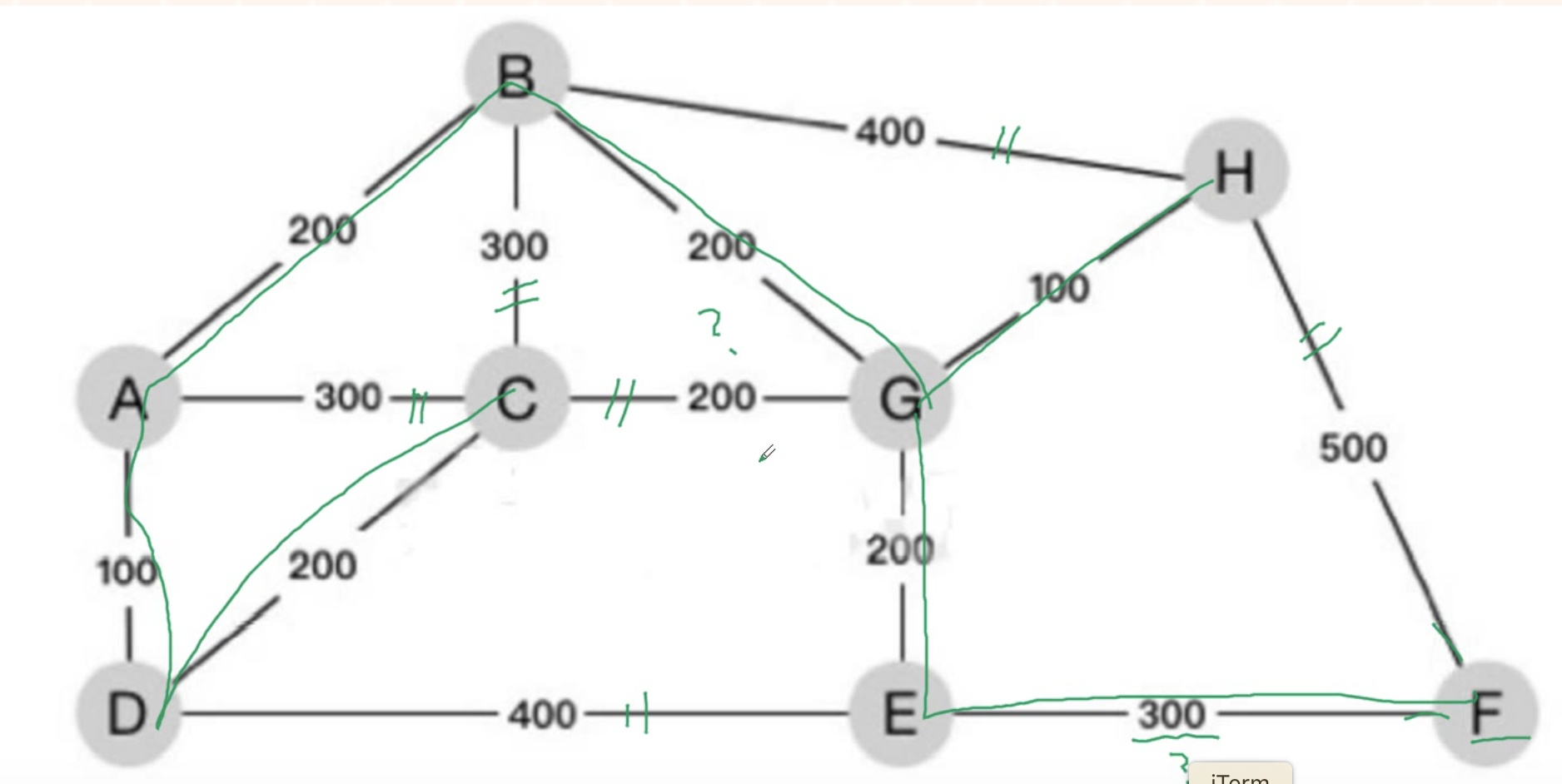
选D

4、匈牙利法

某项目有1、I、II、IV四项不同任务，恰有甲、乙、丙、丁四个人去完成各项不同的任务，由于任务性质及每人的技术水平不同，他们完成各项任务所需时间也不同，具体如下表所示: 项目要求每个人只能完成一项任务，为了使项目花费的总时间最短，应该指派丁完成()任务。

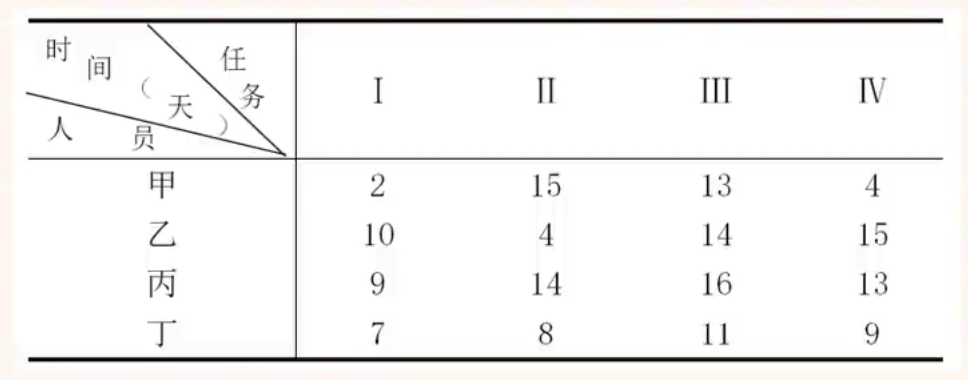
A.I B.II C.III D.IV

解题：

原矩阵

[
 [2, 15, 13, 4],
 [10, 4, 14, 15],
 [9, 14, 16, 13],
 [7, 8, 11, 9],
]

行变换,减去最小值

[
 [2, 15, 13, 4],  // 2
 [10, 4, 14, 15], // 4
 [9, 14, 16, 13], // 9
 [7, 8, 11, 9],   // 7
]

=>

[
 [0, 13, 11, 2], 
 [6, 0, 10, 11],
 [0, 5, 7, 4],
 [0, 1, 4, 2],
]

列变换,减去最小值

[
 [0, 13, 11, 2], 
 [6, 0, 10, 11],
 [0, 5, 7, 4],
 [0, 1, 4, 2],
]
//0   0  4  2

=>

[
 [0, 13, 7, 0], 
 [6, 0, 6, 9],
 [0, 5, 3, 2],
 [0, 1, 0, 0],
]

最优解：至少和维度数相等的线段可以覆盖所有的零

第2轮以及之后的变换规则：

找未被直线覆盖的最小值k
直线相交处+k，未被直线覆盖元素-k，其余元素不变

例如

[
  [15, 18, 21, 24], // 15
  [19, 23, 22, 18], // 18
  [26, 17, 16, 19], // 16
  [19, 21, 23, 17], // 17
]

进行第一轮变换 =>

[
  [0, 3, 6, 9], 
  [1, 5, 4, 0],
  [10, 1, 0, 3],
  [2, 4, 6, 0], 
]
// 0   1  0  0

=>
[
  [0, 2, 6, 9],
  [1, 4, 4, 0],
  [10, 0, 0, 3],
  [2, 3, 6, 0], 
]

维度为4，3条先可覆盖所有0，不是最优解

进行第二轮变换

[
  [-0, 2, 6, -9],
  [-1, 4, 4, -0],
  [-10, -0, -0, -3],
  [-2, 3, 6, -0], 
]

k = 2

[
  [-0, -0, -4, -9],
  [1, 2, 2, -0],
  [-12, -0, -0, -5],
  [2, 1, 4, -0], 
]

此时：维度为4，3条先可覆盖所有0，不是最优解

进行第三轮变换

[
  [-0, -0, -4, -9],
  [1, 2, 2, -0],
  [-12, -0, -0, -5],
  [2, 1, 4, -0], 
]

k = 1

[
  [-0, -0, -4, -10],
  [-0, -1, -1, -0],
  [-12, -0, 1, 5],
  [-1, -0, -3, -0], 
]

此时：维度为4，4条先可覆盖所有0，是最优解

最短路径

网络与最大流量

减枝法

任选路径求最大运力
重复，直到没有通路
最大运力相加

决策论

乐观主义准则大中取大
悲观主义准则小中取大
后悔值准则

后悔值 = 列最大值 - 各个值

后悔值矩阵行大中取小

例如：

[800, 200, -300] 
[600, 250, -150]
[450, 200, -100]
[300, 100, -20]

后悔值：[800, 250, -20]

后悔值矩阵

[0, 50, 280]  max=280
[200, 0, 130] max=200
[350, 50, 80] max=350
[500, 150, 0]  max=500

min(max) = 200

伏格尔法

步骤：

行差、列差：计算同行、同列最小与次最小之差
最大差列或行的最小运价，最大限度满足需求，库存清空则删除该列或行

[
  [4, 12, 4, 11] 32, // 4 - 4 = 0
  [2, 10, 3, 9] 20,  // 3 - 2 =1
  [8, 5, 11, 6] 44,  // 6 - 5 = 1
  // 16  28 28 24
  // 4 - 2 = 2; 10 - 5 = 5; 4 - 3= 1; 9 - 6 = 3
]

max = 5

=>

[
  [4, 12,  4, 11] 32
  [2, 10, 3, 9] 20
  [8, 5, 11, 6] 44 - 28 = 16
// 16  28-28=0 28  24
]


[
  [4,  4, 11] // 4-4=0
  [2,  3, 9]  // 3-2=1
  [8, 11, 6]  // 8-6=2
]
// 4 - 2 = 2;  4 - 3= 1; 9 - 6 = 3

max = 3

[
  [4,  4, 11] 32
  [2,  3, 9]  20
  [8, 11, 6]  16 - 16 = 0
// 16  28   24 - 16 = 8
]

=>

[
  [4,  4, 11] 4- 4 = 0
  [2,  3, 9]   3-2=1
  // 4-2=2; 4-3=1; 11-9=2
]

max=2


[
  [4,  4, 11] 32
  [2,  3, 9]  20 - 16 = 4
// 16 - 16=0  28  8
]

=>

[
  [4, 11] // 11-4=7
  [3, 9] // 9-3=6
// 4-3=1; 11-9=2
]

max= 7

[
  [4, 11] 32-28 = 4
  [3, 9]  4
 // 28-28 =0 8
]

=>

[
  [11] 4
  [9]  4
 // 8
]

确定运费 = 数量 x 单价

加工顺序最优排序

某车间需要用一台车床和一台铣床加工A、B、C、D四个零件。每个零件都需要先用车床加工，再用铣床加工。车床与铣床加工每个零件所需的工时如下表（包括加工前的准备时间以及加工后的处理时间）

工时（小时）	A	B	C	D
车床	8	6	2	4
铣床	3	1	3	12

若以A、B、C、D零件的顺序安排加工，则需要32个小时。适当调整零件加工顺序，可使得所需总工时最短。在这种最短工时方案中，零件A在车床上的加工顺序安排在第（1）位，四个零件加工共需要（2）小时

（1）A. 1; B. 2; C:3; D:4

（2）A. 21; B. 22; C:23; D:24

解题方法:

先找到第一道工序里面最短的排第一
再找第二道工序里面最短的排最后
再找第一道工序里面最短的排第二
再找第二道工序最小的排倒数第二 ...

顺序加工需要32个小时：

工时（小时）	A	B	C	D
车床	8	8 + 6 = 14	14 + 2 = 16	16 + 4 = 20
铣床	8 + 3 = 11	14 + 1 = 15	16 + 3 = 19	20 + 12 = 32

解题

加工顺序：C D A B

工时（小时）	C	D	A	B
车床	2	4	8	6
铣床	3	12	3	1

所需时间22小时

工时（小时）	C	D	A	B	-
车床	2C	2C + 4D = 6	6 + 8A = 14	14 + 6B = 20	-
铣床		2 + 3C = 5	6 + 12D =18	18 + 3A = 21	21 + 1B = 22

计算题

沟通渠道

沟通渠道 = ( n * (n -1)) / 2

计划评审技术(三点估算、PERT)正态分布：

34.13%
13.59%
2.14%

口诀：三世一生，一生无酒，情人节

a 乐观时间
b 悲观时间
m 最可能时间

β分布

期望t =  (a + 4 * m + b) / 6

三角分布

期望t =  (a + m + b) / 3

标准差

σ = (b - a) / 6

进度网络计算题概念

六时标图

最早开始时间ES
最早完成时间EF: EF = ES + 工期估算
最迟开始时间LS
最迟完成时间LF: LF = LS + 工期估算
最早时间：正推，正推取最大
最迟时间：逆推，逆推取最小

单代号网络图，从第0天开始

浮动时间 = 总浮动时间 = 总时差 (不会影响总工期)

浮动时间 = 最晚 - 最早 = LS - ES = LF - EF

自由浮动时间 = 自由时差（不影响紧后活动最早开始时间的最大值）

自由浮动时间 = min(紧后活动ES) - 活动的EF

关键路径：

所有从开始到结束的路径中，活动历时之和最大的路径
项目中所有路径最长的路径，一个项目可以有多个关键路径
关键路径上的总时差为0

总工期：关键路径活动历时之和

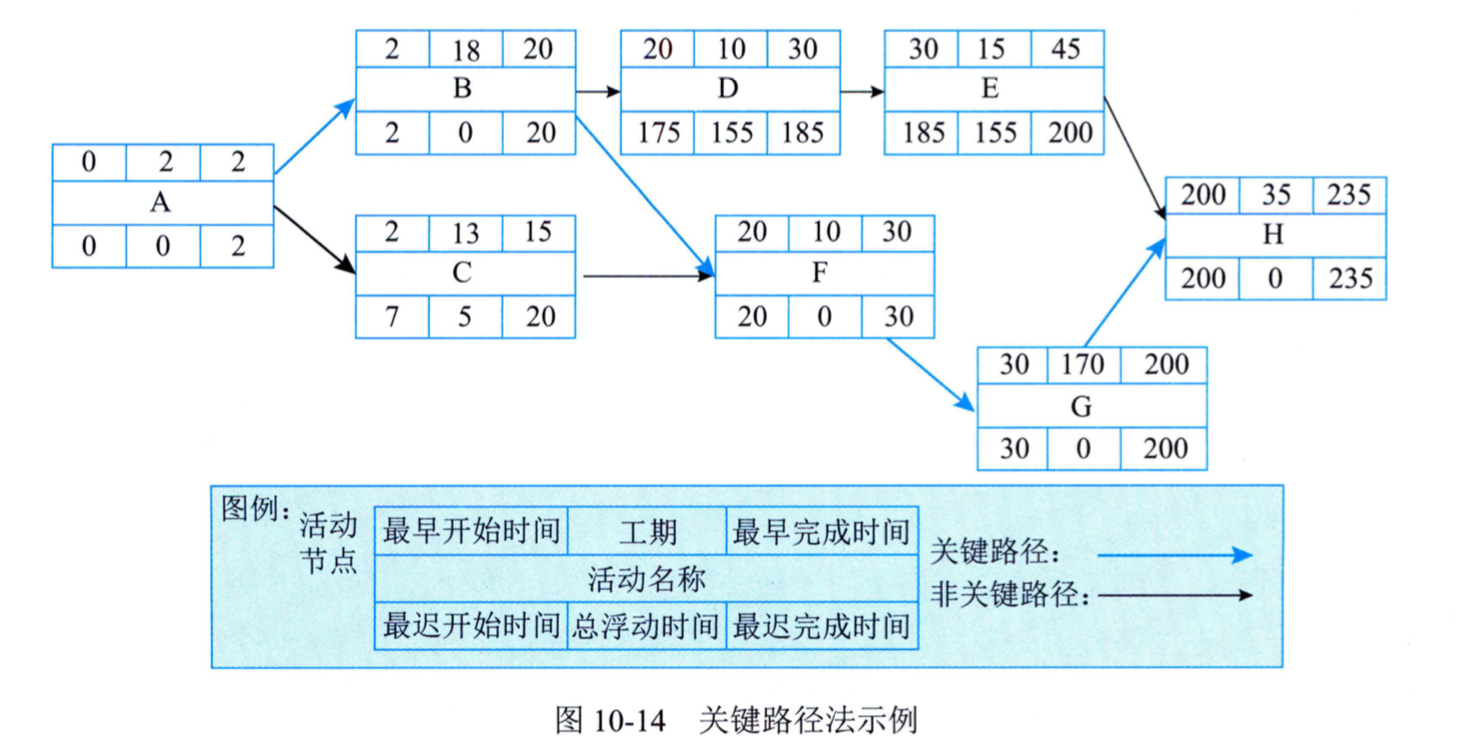
双代号时标网络图

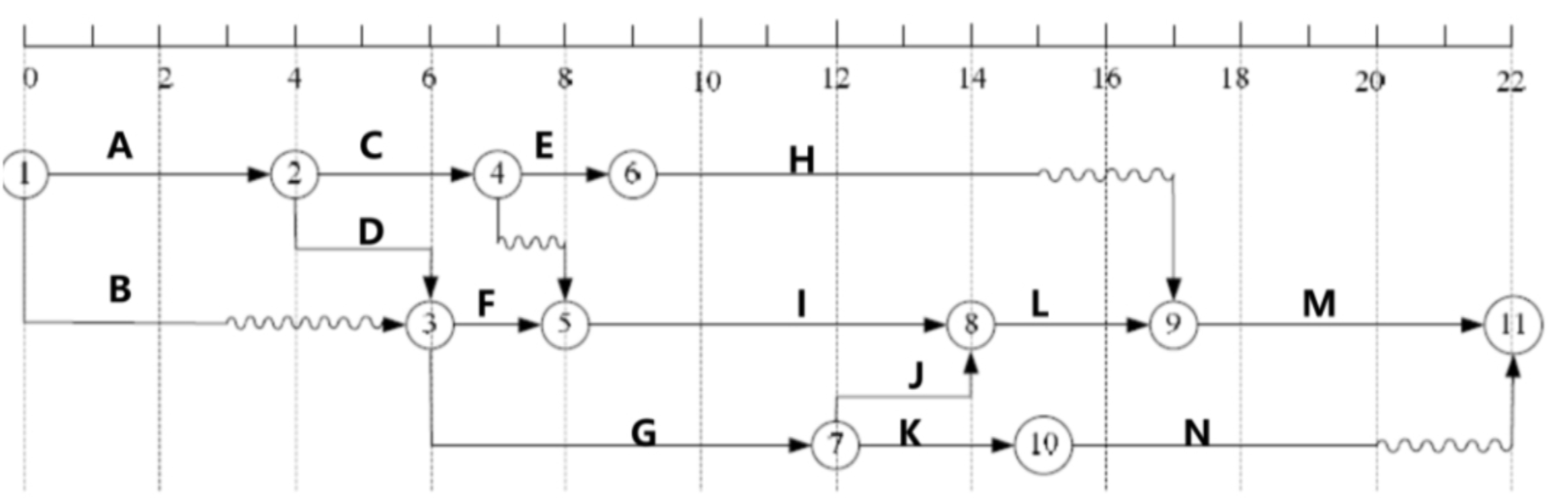
关键路径：波浪线代表该活动的自由时差每个活动的总时差=从该活动开始后续所有路径波浪线之和最小值

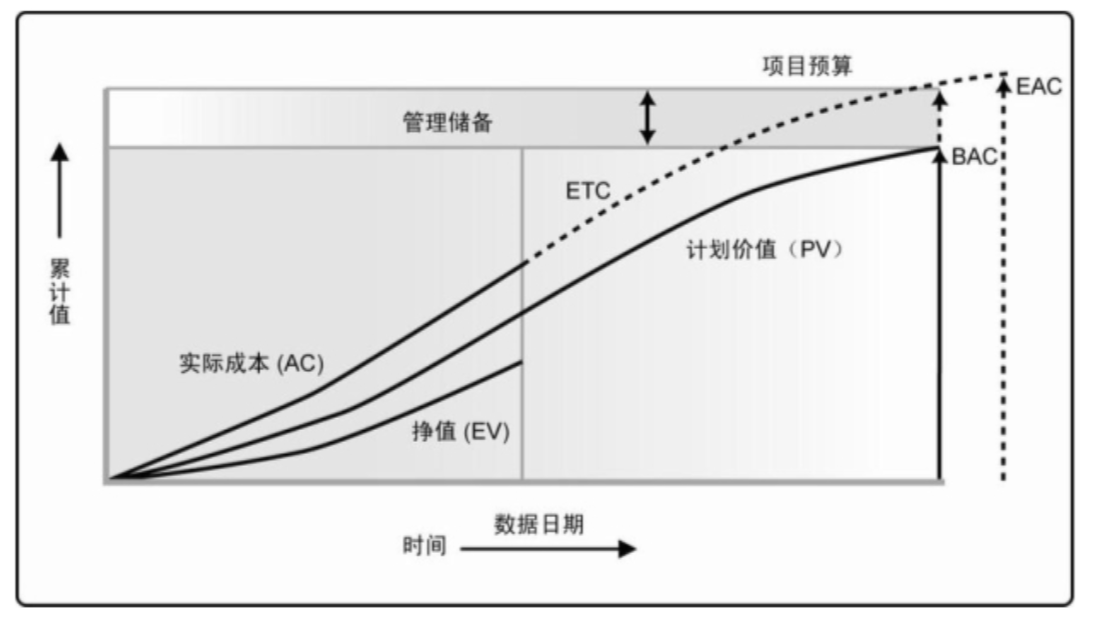
挣值分析

三个指标：

PV （planned value）计划价值（经批准的预算，不包括管理储备）
EV （earned value）挣值已完成工作的测量值（EV <= PV）
AC （actual cost）实际成本

四个计算

CV 成本偏差公式：CV = EV - AC
SV 进度偏差公式：SV = EV - PV
CPI 成本绩效指数公式：CPI = EV / AC
SPI 进度绩效指数公式：SPI = EV / PV

偏差:

偏差 > 0: 进度超前、成本节约
偏差 < 0: 进度落后、成本超支

绩效指数:

绩效指数 > 1: 进度超前、成本节约
绩效指数 < 1: 进度落后、成本超支

EV在左边，越大越好

进度超前 EV > PV、SV > 0、SPI > 1
成本节约 EV > AC、CV > 0、CPI > 1
BAC 完工预算项目的总计划价值
- 计算：BAC = sum(PV)（不包括管理储备）
- 关系：项目预算 = BAC + 管理储备
ETC 完工尚需估算
- 非典型偏差（以后不会再发生类似偏差） ETC = BAC - EV
- 典型偏差（当前偏差可代表未来的趋势） ETC = (BAC - EV) / CPI
EAC 完工估算
- EAC = AC + ETC
- 非典型 EAC = AC + BAC - EV
- 典型 EAC = AC + (BAC - EV) / CPI = BAC / CPI
VAC 完工总偏差
- VAC = BAC - EAC 基于非典型偏差
TCPI 完工尚需绩效指数
- 计算：TCPI = 剩余工作 / 剩余资金
- 基于BAC: TCPI = (BAC - EV) / (BAC - AC)
- 基于EAC: TCPI = (BAC - EV) / (EAC - AC)
PMB 绩效测量基准 PV的总和

预测技术

进度落后，成本超支可以采取的措施

(1) 用高效人员代替低效人员;
(2) 加班或赶工在预防风险的情况下并行施工;
(3) 提高资源利用率:
(4) 加强、改进沟通，提高效率;
(5) 尽可能一次性把事情做对，减少返工。
(6) 加强沟通
(6) 增强优质资源
(7) 外包和缩小项目范围

进度落后，成本节约可以采取的措施 (1) 赶工(例如全体加班方式) 加快进度 (2) 使用高效资源来替换低效资源加快进度 (3) 改进方法，提高工作效率

进度超前，成本超支可以采取的措施: (1) 整个项目需要抽出部分人员以放慢工作进度; (2) 整个项目存在成本超支现象，需要采取控制成本措施: (3) 项目中区分不同的任务，采取不同的成本及进度措施: (4) 必要时调整成本基准。 (5) 优化施工方案、提高效率、加强质量管理减少返工、加强沟通，以降低成本; (6) 在确保进度按期完成的基础上，可以降低进度以节约成本; (7)总结项目进度“提前”的经验，并记录下来，把这经验传播到项目的其他班组，甚至其他项目或未来的项目:

进度超前，成本节约可以采取的措施: (1) 抽调部分人员用于其他项目 (2) 加强质量控制，密切监控项目 (3) 必要时调整计划或基准等方法改进，或者改变相关计划

https://www.bilibili.com/video/BV1wh4y1M74f/?p=68&spm_id_from=pageDriver&vd_source=efbb4dc944fa761b6e016ce2ca5933da

第21章 项目管理科学基础 ​

21.1 工程经济学 ​

21.1.1 资金的时间价值与等值计算 ​

21.1.2 项目经济评价 ​

21.2 运筹学 ​

21.2.1 线性规划 ​

21.2.2 运输问题 ​

21.2.3 指派问题 ​

21.2.4 动态规划 ​

21.2.5 图与网络 ​

21.2.6 博弈论 ​

21.2.7 决策分析 ​

考点 ​

1、线性规划 ​

2、动态规划 ​

3、最小生成树 ​

4、匈牙利法 ​

最短路径 ​

网络与最大流量 ​

决策论 ​

伏格尔法 ​

加工顺序最优排序 ​

计算题 ​